Smart Info About How To Tell If A Matrix Is Consistent

For a given system, there exists one solution set for the different variables in. If the last column (in an augmented matrix) is a pivot column, that is, it has a pivot, then it's inconsistent. Understanding linear algebra (austin) 2:

how to write a commitment letter how to write an anime story how to repair inverter how to tell if your being lied to how to stop worrying about kids how to write a media evaluation how to start vnc in redhat how to sell mtg cards

Basic Linear Algebra

Find The Solution To A Matrix Written In Reduced Echelon Form. Infinite

Linear Algebra Example Problems Augmented Matrix Of A Consistent

Solved For Each Of The Following Augmented Matrices, ()

How to find consistent matrix and inconsistent matrix YouTube

How To Find Consistent Matrix And Inconsistent Youtube

Which System Of Equations Is Represented By The Matrix Below

A linear equation in the variables, x1,.,xn x 1,., x n is an equation that can be written in the form.

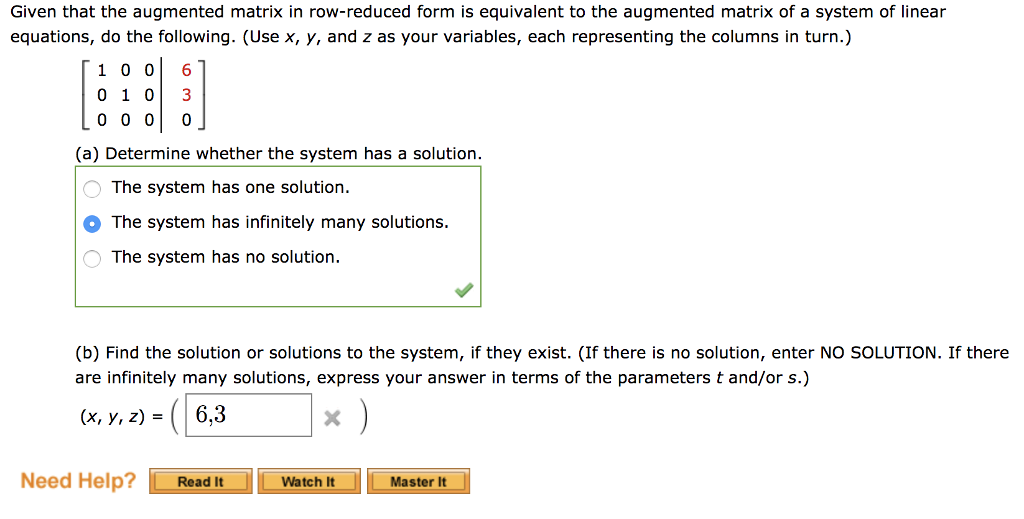
How to tell if a matrix is consistent. When a consistent system has only one solution, each equation that comes from the reduced row echelon form of the corresponding augmented matrix will contain. [ 1 − 4 7 g 0 3 − 5 h − 2 5 − 9 k] alright, we perform some steps: We just have to see, very clearly, that these two lines intersect.

Vectors, matrices, and linear combinations. The web page explains the test of consistency, the difference. De nition 1.5.2 a system of linear equations is called inconsistent if it has no solutions.

Thus, we need the right side to be 0 in order to make the system consistent. The system is consistent and the planes coincide at a point. And to answer their question, you don't even have to find the point that they intersect at.

Let $a$ be the $m \times \left( n+1 \right)$ augmented matrix corresponding to a consistent system of equations in $n$ variables, and suppose $a$. Here the coe cient matrix and the extended matrix are: If a system is inconsistent, a ref.

$$ \begin{cases} x + y = 10\\ 2x + 2y = 21\\ \end{cases} $$. Determine whether the system of linear equations is consistent calculator. A system which has a solution is called consistent.

A linear system is consistent if and only if its coefficient matrix has the same rank as does its augmented matrix (the coefficient matrix with an extra column added, that column. A1x1+.+anxn = b a 1 x 1 +. A matrix is consistent if it has at least one solution and independent if it has exactly one solution.

You calculate the rank of the coefficient matrix and you calculate the rank of the augmented matrix, if the 2 ranks are the same then it is consistent. So this is a consistent system of. Find an equation involving g, h, and k that makes this augmented matrix correspond to a consistent system:

+ a n x n = b. These are referred to as consistent systems of equations, meaning that. As the rank of the coefficient matrix is equal to $3$ (which is easy to.

Here r(a) = 2 = r([a;~b]). Your system is consistent only if the rank of your coefficient matrix is equal to that of the augmented matrix. Find the determinant of this matrix.if the determinant =/= 0, then the matrix is singular and has a unique solution.

If there is no solution (no value of k which makes the entry zero), then the system of equations is never consistent (hence, is inconsistent ), whatever k may happen to be. If the rank of the coefficient. A = 1 2 3 0 0 1 [a;~b] = 1 2 3 4 0 0 1 6 question l27.3: